반응형
Chapter 01. 기초통계_기초과정
추정(Estimation) – 모비율/모평균/모분산 추정 완전 정리
1. 주요 개념 요약
① 점추정 & 구간추정
- 점추정: 모수가 가질 값 하나를 추정
- 구간추정: 모수가 존재할 가능성이 있는 구간을 제시
- 신뢰수준 95% → 오차가 발생할 확률 5% → 유의수준 α = 0.05
② 모비율(p)의 점추정 & 분산
비율(class)이 1이면 성공, 0이면 실패라고 둘 때
표본에서 성공한 개수 X ~ B(n, p)
- 점추정량: p̂ = X/n
- 기대값: E(p̂) = p
- 분산: Var(p̂) = p(1-p)/n
③ 모비율 구간추정
CLT 조건 필요:
- np > 5
- n(1 – p) > 5
신뢰구간 공식:

④ 모비율 차이(p₁ – p₂) 추정
- 점추정: p̂₁ – p̂₂
- 분산:
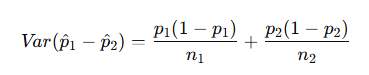
신뢰구간:

⑤ 모평균 차이(μ₁ – μ₂) 추정
- 점추정: X̄₁ – X̄₂
- 분산:

모분산을 알고 있을 때:

모분산을 모를 때:
- 등분산 가정 → 합동분산 사용

t 분포 이용:

⑥ 모비율 표본 크기 계산
오차 d를 허용할 때:

p(1-p)의 최대값은 1/4 → 가장 보수적 계산 가능
2. 코드 예시 (Python)
import math
from scipy.stats import norm, t
# 모비율 신뢰구간
def proportion_ci(phat, n, alpha=0.05):
z = norm.ppf(1 - alpha/2)
se = math.sqrt(phat * (1 - phat) / n)
return phat - z * se, phat + z * se
# 모비율 차이 신뢰구간
def diff_proportion_ci(p1, n1, p2, n2, alpha=0.05):
z = norm.ppf(1 - alpha/2)
se = math.sqrt(p1*(1-p1)/n1 + p2*(1-p2)/n2)
diff = p1 - p2
return diff - z * se, diff + z * se
# 모평균 차이 신뢰구간 (등분산 가정)
def diff_mean_ci_equal_var(x1, s1, n1, x2, s2, n2, alpha=0.05):
df = n1 + n2 - 2
sp2 = ((n1-1)*s1**2 + (n2-1)*s2**2) / df
sp = math.sqrt(sp2)
t_val = t.ppf(1 - alpha/2, df)
diff = x1 - x2
se = sp * math.sqrt(1/n1 + 1/n2)
return diff - t_val * se, diff + t_val * se
* 이 글은 제로베이스 데이터사이언스 파트타임 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다.
💡 생각 정리
이번 단원에서는 비율·평균·분산에 대한 점추정과 구간추정 전체 흐름을 하나로 연결해서 이해하게 되었다.
특히 모비율은 이항분포 → 정규근사 → CLT 조건이라는 구조가 중요하고, 모평균 차이는 모분산을 알고 있는지/모르는지, 모르는 경우 또 등분산 여부에 따라 추정 방식이 달라진다는 점이 핵심이다.
또한 신뢰구간의 구조가 대부분 “점추정량 ± 임계값 × 표준오차” 형태로 통일된다는 패턴을 확실히 잡을 수 있었다.
🚀 적용점
- 설문조사, 사용자 행동 데이터 분석(전환률, 클릭률 등)에서 바로 활용 가능
- A/B 테스트에서 p₁ – p₂ 차이를 검정할 때 기초 로직이 동일
- 마케팅·서비스·제품 기획에서 모평균 비교로 유의한 차이가 있는지 파악 가능
- 신뢰구간을 활용해 “얼마나 정확한 추정인가”를 판단하고 보고서 작성 시 근거 제시 가능
- 표본 크기 계산 공식은 실제 조사 기획 시 반드시 필요한 기준이 됨
반응형
'데이터' 카테고리의 다른 글
| 제로베이스 데이터사이언스 스쿨 - Part 04. 기초 통계-12 (0) | 2025.11.19 |
|---|---|
| 제로베이스 데이터사이언스 스쿨 - Part 04. 기초 통계-11 (0) | 2025.11.18 |
| 제로베이스 데이터사이언스 스쿨 - Part 04. 기초 통계-9 (0) | 2025.11.16 |
| 제로베이스 데이터사이언스 스쿨 - Part 04. 기초 통계-8 (0) | 2025.11.15 |
| 제로베이스 데이터사이언스 스쿨 - Part 04. 기초 통계-7 (0) | 2025.11.14 |